Lagebeziehung von Geraden
# Einstieg
# Sicherung
Zwei Geraden $g$ und $h$ mit $$ g:\vec{u}+s\cdot\vec{v} $$ $$ h:\vec{l}+t\cdot\vec{m} $$
können die folgenden Lagebeziehungen zueinander haben:
# parallel
Zwei Geraden sind parallel, wenn ihre Richtungsvektoren kollinear sind.
Mathematisch zu überprüfen ist: Existiert ein $x$, so dass gilt: $$ \vec{v}=x\cdot \vec{m} $$
# identisch
Zwei Geraden sind identisch, wenn sie parallel sind und der Stützvektor einer Geraden auf der anderen Geraden liegt.
Mathematisch zu überpüfen ist: Existiert ein $s$, so dass gilt: $$ \vec{l}=\vec{u}+s\cdot\vec{v} $$ oder analog: Existiert ein $t$, so dass gilt: $$ \vec{u}=\vec{l}+t\cdot\vec{m} $$
# sich schneidend
Zwei Gerade schneiden sich, wenn ihre Richtungsvektoren nicht kollinear sind und es einen Punkt auf der Geraden $h$ gibt, der gleichzeitig auch auf der Geraden $g$ liegt.
Mathematisch zu überprüfen ist: Existieren $s$ und $t$, so dass gilt: $$ \vec{l}+t\cdot\vec{m}=\vec{u}+s\cdot\vec{v} $$
# windschief
Zwei Geraden sind windschief zueinander, wenn ihre Richtungsvektoren nicht kollinear sind und sie sich nicht schneiden.
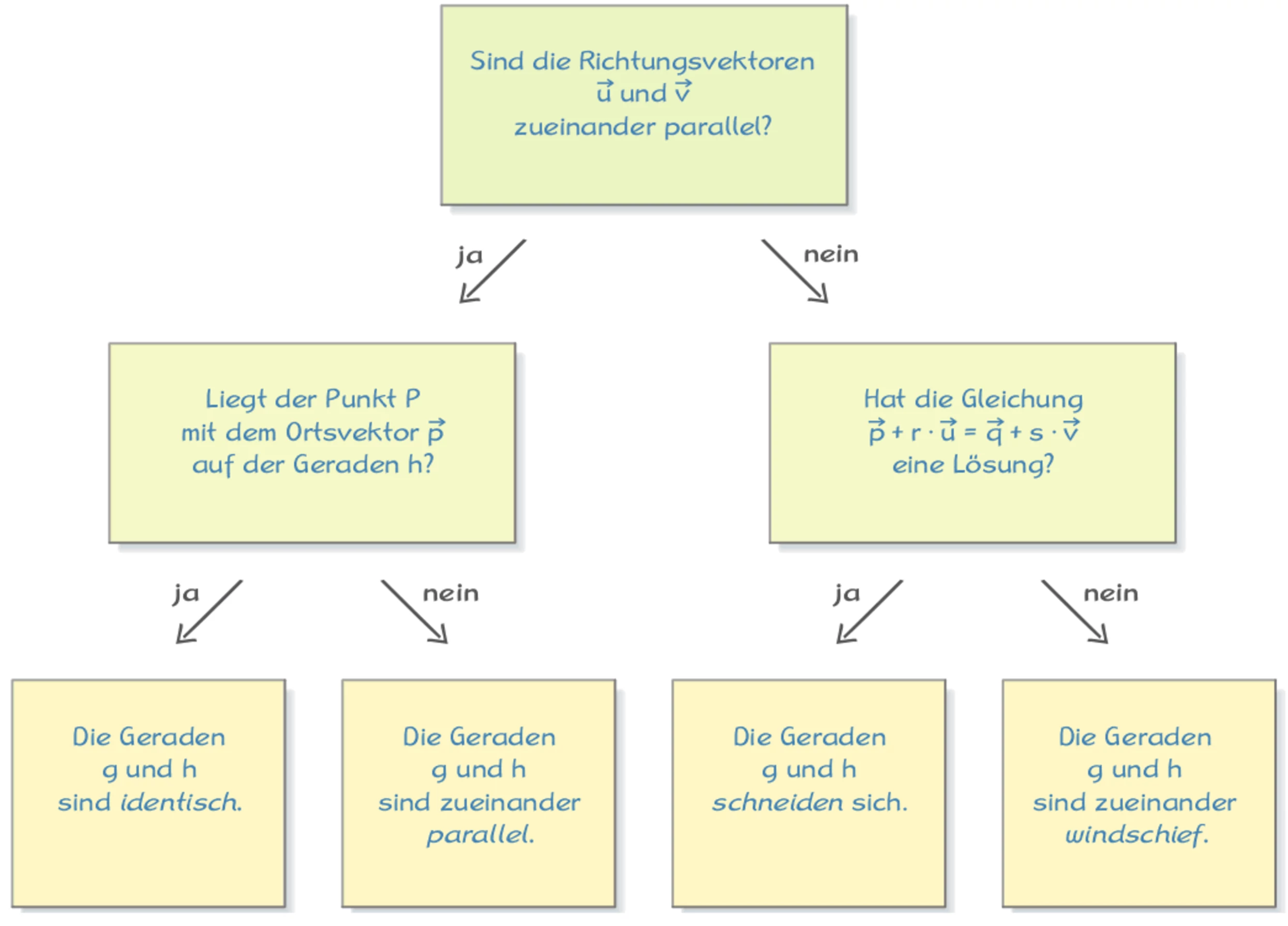
# Entscheidungsbaum für die Lagebeziehung
Der folgende Entscheidungsbaum stellt eine sinnvolle Reihenfolge zur Überprüfung der Lagebeziehung zwischen zwei Geraden dar: