Die beschleunigte Bewegung
# Aufnahme der Bewegung
# Messwerte
Hier der Link zu einem Teil der Messwerte:
Hier die Messwerte zur Ansicht:
| Zeit (in s) | x (in m) |
|---|---|
| 0 | 0 |
| 0.4117 | 0.013372 |
| 0.8117 | 0.050202 |
| 1.212 | 0.111412 |
| 1.612 | 0.186812 |
| 2.012 | 0.277412 |
| 2.412 | 0.369812 |
| 2.812 | 0.464012 |
| 3.212 | 0.565312 |
| 3.613 | 0.669012 |
| 4.013 | 0.772912 |
| 4.413 | 0.873112 |
# Auswertung der Bewegung
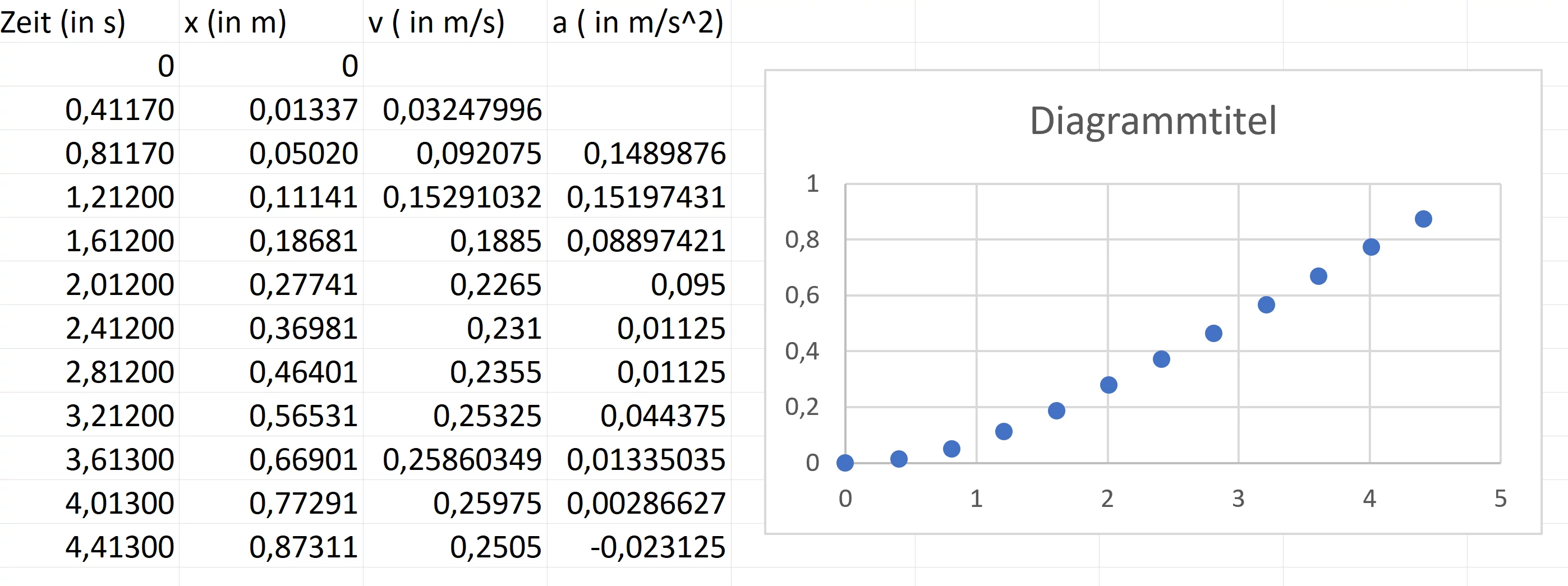Weder bei der Geschwindigkeit, noch bei der Beschleunigung existiert ein erkennbares Muster.
Eventuell einfach eine schlechte Messung?
=> Bessere Messung erstellt!
# Messergebnisse eines abgewandelten Experiments
Die folgenden Messwerte entstanden bei von den SuS durchgeführten Experimente mit Hilfe der Videoanalysesoftware
Viana2:
(Da csv-Dateien nicht im Browser dargestellt werden: Rechtsklick/Langklick auf das Symbol und “öffnen in neuem Tab”)
# Auswertung
Von den Messungen hatte die Datenreihe von Yarens Gruppe die “besten” Messwerte.
Diese waren wie folgt (schon leicht formatiert):
| Zeit (in s) | s (in m) | v (in m/s) | a (in m/s^2) |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0.03331 | 0.1633 | ||
| 0.1332 | 0.3745 | 2.11432575833417 | |
| 0.1998 | 0.5767 | 3.03603603603604 | 13.8394936591872 |
| 0.2665 | 0.8263 | 3.74212893553223 | 10.5861004422219 |
| 0.3331 | 1.11 | 4.25975975975976 | 7.77223459801093 |
| 0.3997 | 1.432 | 4.83483483483483 | 8.63476088701309 |
| 0.4663 | 1.796 | 5.46546546546547 | 9.46892838784737 |
| 0.5329 | 2.181 | 5.78078078078078 | 4.73446419392355 |
Um aus Daten in Tabellen Muster erkennen zu können ist es hilfreich, sie zu plotten (in ein Diagramm zu übertragen)
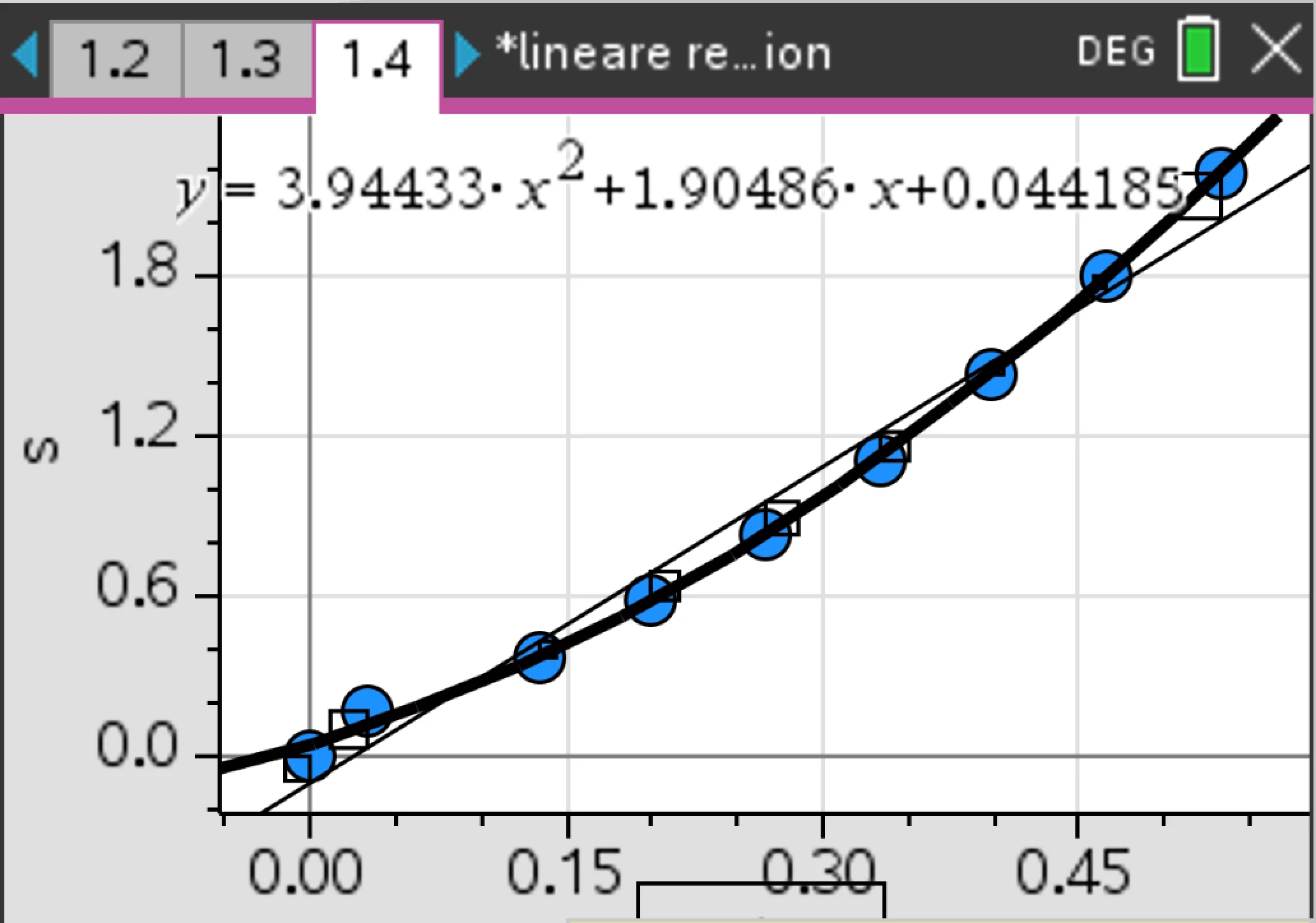
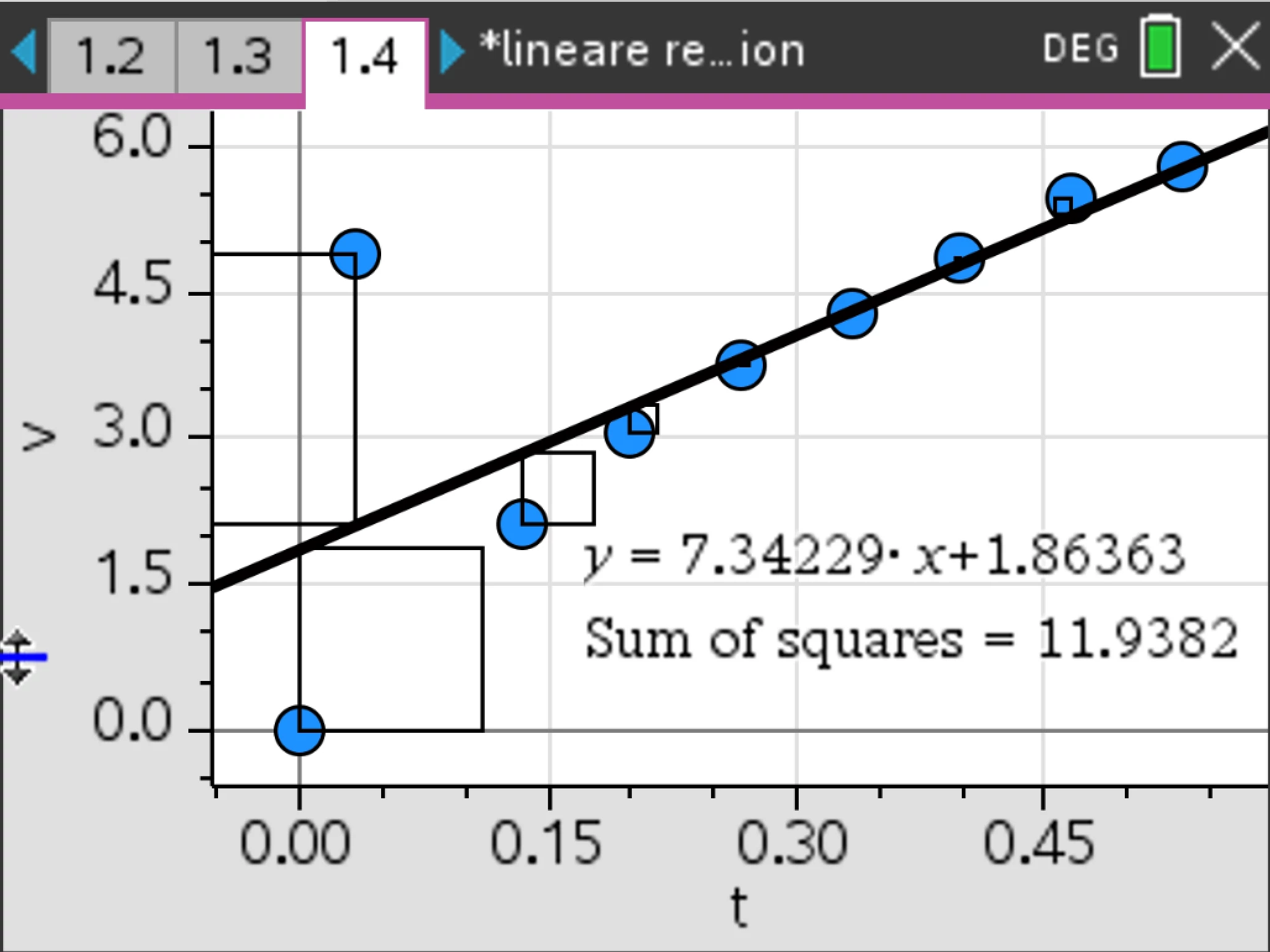
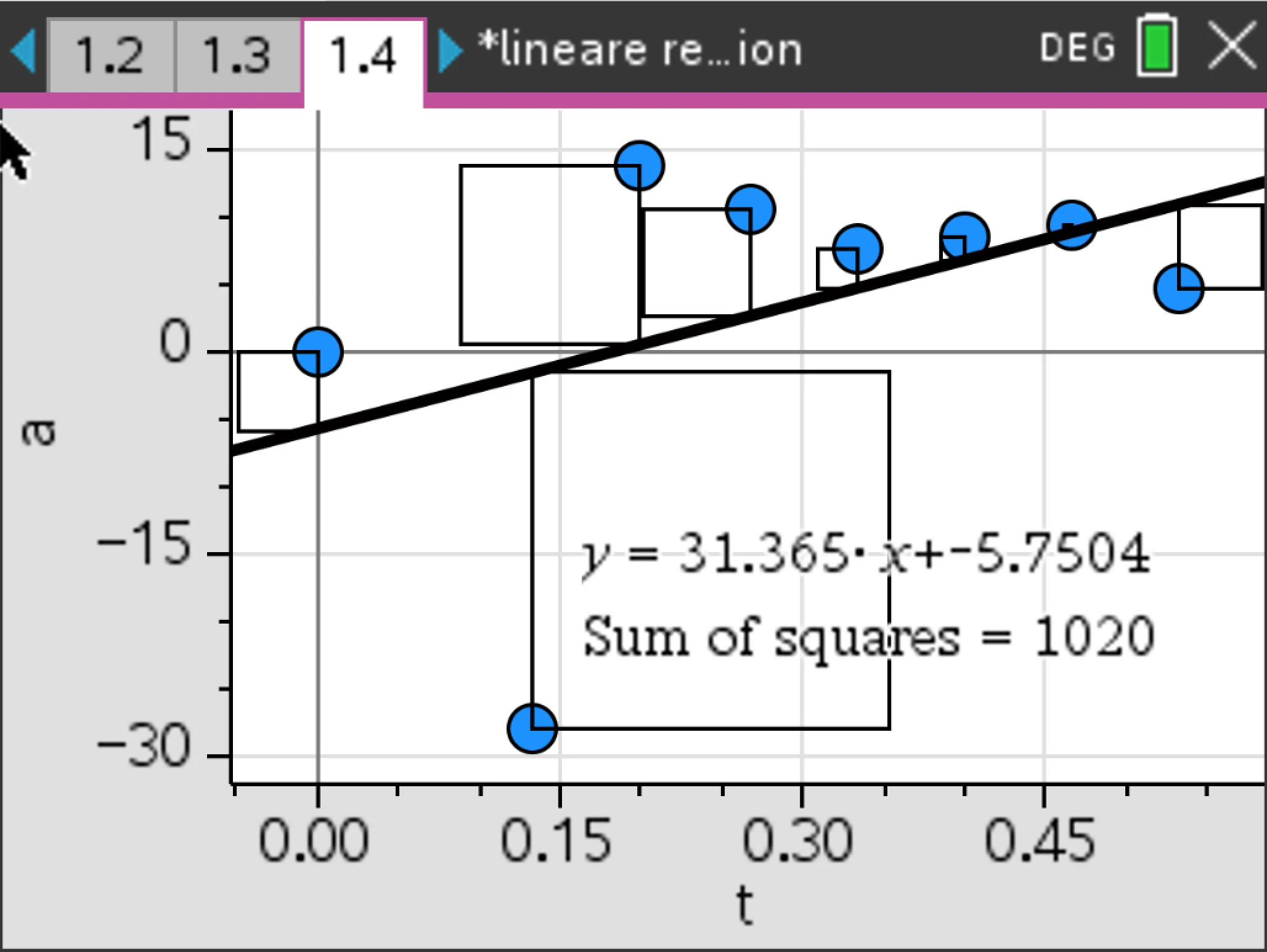
Es lässt sich erkennen, dass die Messwerte im t-s-Diagramm näherungsweise quadratisch verlaufen, eine Funktion $$ s(t)=k\cdot t^2, $$ mit einem passenden Wert für $k$, in der Lage ist, den Verlauf der Messwerte zu beschreiben.
Dimensionsüberlegungen führen uns für die Einheit von $k$ zu $\frac{m}{s^2}$ , da $s(t)$ die Einheit $m$ und $t^2$ die Einheit $s^2$ hat.
Die Beschleunigung $a$ der Bewegung können wir im t-v-Diagramm als Steigung der Geraden erkennen (Erinnerung: Beschleunigung ist die Änderung der Geschwindigkeit pro Zeiteinheit). Da $k$ und $a$ die gleiche Dimension (und Einheit) hat, lohnt sich ein Vergleich:
Der Faktor $k$ sieht ungefähr halb so groß aus, wie die Beschleunigung $a$.
These: Für die Bewegungsgleichung der geradlinigen gleichförmig mit konstanter Beschleunigung gilt: $$ s(t)= \frac12 a t^2 $$ Dies gilt es mit einem besseren Experiment erneut zu überprüfen!